1�D�͂��߂�
���̓x�i��Ёj�t���[�h�p���[�V�X�e���w����2022�N�w�p�_���܂��������������ƁC�����҈ꓯ�ɂƂ��Đg�ɗ]����h�ł���D���Y�_���͒���Ɠ����ʼnY�H�Ƒ�w�@���H�w�����ȏC�m�݊w�i���g���^�����ԁj�̈ɓ����C�ʼnY�H�Ƒ�w�V�X�e�����H�w�������̑��R�h���C���K�j�S���̋����ł���C���̋@��ɓ��Y�����Ɋւ���v���o��⑫�I�Ȑ������𒆖삪��\���ď����Ƃǂ߂�D
�����̂��������͏\���N�ȏ�O�ɑk��D���삪�ʼnY�H�Ƒ�w���N�ސE�����R�ȓ��X���߂����Ă�������C�{�w��uOHC-Sim�Ɋւ��錤���ψ���v�W�̉�ŋ�C���ǘH����헬�ɂ��ē����o�����͔�E���ʓ������ȒP�ɕ\���ł���Z�o�����������Ƃ��b��ƂȂ����D��������������ɓ��Z�o���̓��o�ɋ�����������ꂽ�D�����ŋ�C���ǘH����헬����Ǔ����k�����̈ꎟ����헬��Ƃ��Ēu�������C���̗��ʓ�����\���ł���V�~�����[�V�������f���\�z�Ɋւ��鋤���������ōH���N�ސE�̒���ƌ��E�̐��Ŏn�߂邱�Ƃɂ����D�Ǔ����ɂ��Ă�1930�N�㏉��Prandtl, Nikuradse, Karman�炩��n�܂�C���̌㒷�N�ɂ킽�葽���̌����ғ��ɂ�鐬�ʂ����\����Ă��Ă���D����Ӗ��Łu��C���������v�ɍ��X���g�ވӖ�������̂��Ǝ��₵�Ȃ���̑D�o�ƂȂ����D
����ISO 6358�ł͈��k�����̗p�@��̗��ʓ��������@����������Ă����D���̒��ň�ʋ�C���@�헬�ʓ����͉����R���_�N�^���X�C�ՊE�w���C�������w���C�N���b�L���O���͂̂S�p�����[�^��p���ĕ\���ł���Ƃ����D�������`��͒P������������C���ǘH�̗��ʓ����͂��قȂ邱�Ƃ������������ʕ�1)������Ă����D�����ʼn�X�͐悸��n�߂ɁC�f�M�E�����������ΏۂƂ���Fanno����̗��ʓ�����\���ł���V�~�����[�V�������f�����Ă����̗L�������m���߁C���ŊǕǂ���̔M�`�����l����������ւƌ����W�����Ă����D
�Q�D�ꎟ�����Ǔ�����̃V�~�����[�V�������f��
2.1�@��{��
�@���Y�_���ł͊Ǖlj��xTw�����ɕۂ��ꂽ���aD���E�^���~�Ǔ���C��헬����ꎟ������Ƃ��ċߎ��I�Ɉ�����@�ɕ�����D�ǕǂƂ̖��C�ƔM�̎�����l�������ꎟ���E��������E��헬��̉^���ʕۑ��Ɋւ����b���́i�P�j���ŕ\�����D�Ǔ������C�m���Y��Re�͎��ʗ��ʂƔS�x�Ƃ̔�Œ�܂�D�ǘH�ɉ����Ă̋�C�S�x�ω��͏������Ƃ��āC�S�x�͂��̕��ϒl�ň��Ƃ���D���������ă��C�m���Y��Re�̊��Ƃ���Filonenko�̋ߎ������ɂ���Ă�������ꖀ�C�W��f�͈��l�Ƃ���D
�����ƔM�̈ړ��Ɋւ��鑊�����ɂ��Chilton-Colburn�̃A�i���W�[���ߎ��I�ɓK�p�ł���Ɖ��肷���dx��dT0���܂ށi�P�j���E�ӂ́i�Q�j���E�ӂ̂悤��dx�Ɋւ��鍀�݂̂ŕ\�����`�ɂȂ�D������Pr�̓v�����g�����ň��l�DT�͊Ǔ���C�É��x�ŊǓ��������̈ʒux�ɂ��ω�����D���̕ω��̑�܂��ȗl�q��m�邽�߂�Notter
& Sleicher
2)�̗���Graetz���ɑ����![]() �ɂ�鐄����}�P�Ɏ����D�Ǔ��������̖�����������x/D�ɑ��Ĕj���C��_�����Ŏ������Ȑ��͊ǘH�ɉ�������C���x�ω����������x�ƊǕlj��x�Ƃ̍��Ŗ����������Ď��������̂ł���D���ꂼ�ꖳ�������x�ω���0����0.9�ɒB����܂ł̋�ԁi���Q�Ɓj�ł͉��x�ω����������ǕǂƂ̔M�`�B���l�����Ȃ���Ȃ�Ȃ��D����C���������x�ω���0.9����1.0�ɒB�����Ԃł͔M�`�B�̉e�����������f�M����ŋߎ�����ƁC�S���x�͕ς�炸dT0=0�Ȃ�C�i�P�j���́CFanno����̎��Ɠ���ɂȂ�D�����ŊǘH�������ɋ߂��ǕǂƂ̓`�M���l�������ԂƂ��̉������Ɉ��������ڑ�����f�M����ŋߎ������ԂƂɊ�{�����čl����D
�ɂ�鐄����}�P�Ɏ����D�Ǔ��������̖�����������x/D�ɑ��Ĕj���C��_�����Ŏ������Ȑ��͊ǘH�ɉ�������C���x�ω����������x�ƊǕlj��x�Ƃ̍��Ŗ����������Ď��������̂ł���D���ꂼ�ꖳ�������x�ω���0����0.9�ɒB����܂ł̋�ԁi���Q�Ɓj�ł͉��x�ω����������ǕǂƂ̔M�`�B���l�����Ȃ���Ȃ�Ȃ��D����C���������x�ω���0.9����1.0�ɒB�����Ԃł͔M�`�B�̉e�����������f�M����ŋߎ�����ƁC�S���x�͕ς�炸dT0=0�Ȃ�C�i�P�j���́CFanno����̎��Ɠ���ɂȂ�D�����ŊǘH�������ɋ߂��ǕǂƂ̓`�M���l�������ԂƂ��̉������Ɉ��������ڑ�����f�M����ŋߎ������ԂƂɊ�{�����čl����D
![]()
�����ŁCD�F���a�Cx�F�ǎ����W�CM�F�}�b�n���CT0�F�S���x�Cf�FFanning�̖��C�W���C���F��M��
2.2�@�V�~�����[�V�����v�Z���f��
�@�M�`�B�l����Ԃł͋�C���xT��x�Ɉˑ����邱�Ƃ���i�Q�j�������̂܂ܐϕ��ł��Ȃ��D�����ł���߂čr���ߎ��ł͂��邪���̋�Ԃ̕ω������C���x![]() ����ԓ����ς�����\���xTr�i���l�j�Œu�������C�i�Q�j�����i�R�j���̂悤�ȕϐ������`�ɕϊ����Đϕ������@���̗p�����D�i�R�j�����ǒ�L�ɂ킽���Đϕ�����C�ǘH�����C�o���̃}�b�n��M1�CM2�Ɩ��C�W��f�̊W�������܂�D���E����������Z�o����門�C�W��f��M1�ɑ��関�m��M2�����肷�邽�߂ɂ͖{�W�����J��Ԃ��v�Z���ɂ������K�v������D
����ԓ����ς�����\���xTr�i���l�j�Œu�������C�i�Q�j�����i�R�j���̂悤�ȕϐ������`�ɕϊ����Đϕ������@���̗p�����D�i�R�j�����ǒ�L�ɂ킽���Đϕ�����C�ǘH�����C�o���̃}�b�n��M1�CM2�Ɩ��C�W��f�̊W�������܂�D���E����������Z�o����門�C�W��f��M1�ɑ��関�m��M2�����肷�邽�߂ɂ͖{�W�����J��Ԃ��v�Z���ɂ������K�v������D
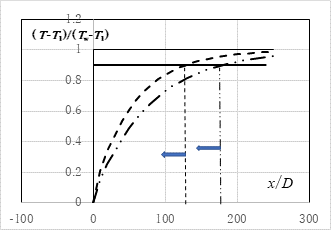
�{�����ł͊ǘH���E�����Ƃ��ĊǕlj��xTw���C�㗬�[�̗�����C�S���xT01����ёS��p01���Ƃ��C������}�b�n��M1��A���I�ɕω������ė^�����ꍇ�̊ǘH�o���}�b�n��M2�ƑS��p02��A���I�ɓ��o�ł���悤MATLAB-Simulink��ɐ��l�v�Z���f�����\�z�����D���̍ہi�R�j���̐ϕ����ʂ��������߂̌J��Ԃ��v�Z�̑����Simulink��ł�M2�����߂�t�B�[�h�o�b�N�ϕ�����n�̒�퉞���𗘗p�����@3)���̗p�����D�ǘH�̗��ʓ��������߂�u���b�N���}�S�̂̊T���͐}�Q�̂悤�ɂȂ�D���̏ڍׂ͏Ȃ����C�^����ꂽ���͏�������u���C�m���Y���������߂�u���b�N�v�C�u�M�`�B���l�������Ԃ̃u���b�N�v�C����ɉ������ɐڑ������u�f�M�ߎ���Ԃ̃u���b�N�v����Ȃ��Ă���D
![]()
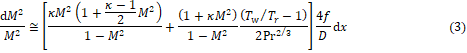
3�D �����ɂ�錟��
3.1�@�������u
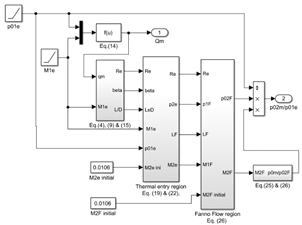
�ǘH�����M�E��p����ݔ��Ƃ��ē����C��C���p�������`���[�u��������␅�����������ɐZ�����Z�b�g��p���������肵���������ʂ�����ꂸ�C�}�Q�Ɏ����悤�ɕۉ��ނŕ�܂ꂽ�����r�j�[���p�C�v���ɉ�����␅�����C���̒��ɋ����ǘH�̓��ǂ�ʂ��C�Ǖlj��x��M�d�ŊĎ�����Z�b�g��p�����D�ʉߎ��ʗ��ʂ̑���͏㗬����C�����Ƃ��ėp���������^���N�����͕ω�����Z�o�������4)�Ɉ˂����D�Ǔ�����o���̈��͑���ł́C�ǘH�ƈ��͑���p�ɓ��a���g�債���ǂ�A������J�ڐڎ�iJIS���ŋK��j��p�ӂł����C��ނ��}�g��ƂȂ�ʏ�̐ڎ�ʼn��p�����D�����Œ��Ǖ������ɑ��čs�����V�~�����[�V�����v�Z�ɂ�������o�����͔�ɋ}�g��̉e�����Z�����Ď����̈��͔�Ɣ�r���邱�Ƃɂ����D�����ɗp�������ǂ̓��a�͓�����o���ő����������邱�Ƃ��炻�̕��ϒl����a�Ƃ��CD=2.025mm��D=3.91mm�̓��ނŁC�ǒ�L������1.1m�̓��ǂ�p�����D
3.2�@��������
�ǘH������C���x�ƊǕlj��x��295K�œ������ꍇ�C�����������͔�Ǝ��ʗ��ʂ̊W���Z��Ŏ������̂��}�S�ŏ㑤���㗬�����̏ꍇ�C�����������[��C�J���̏ꍇ�ł���D�����ɑΉ�����V�~�����[�V�����v�Z��f�M��Fanno����Ƃ��ċ��߂����ʂ��Ȑ��Ŏ����Ă���D���҂��悭��v���邱�Ƃ��m�F���ꂽ�D
�����ŊǘH�����M�E��p���ĊǓ���C���x���傫���ω�����ꍇ�ł��C����ɂ���C�S�x�ω�������Fanno����̌v�Z�Ɏ������C�������ʂɋ߂����f�������ł���̂ł͂Ȃ����Ƃ����^�₪������D����ɂ��Č����������ʂ��}�T�ł���D�����[�S��p01=0.6MPa���C������C�S���xT0=293K�C�Ǖlj��xTw=333K�Ƃ����ꍇ�̎������ʂ�����Ŏ����Ă���D�Ǔ���C�S�x��333K ��293K�ł��ꂼ��]�������ꍇ�̂Q��ނ�Fanno���f���ɂ��v�Z���ʂ͎����Ɣj���Ŏ������Ȑ��̂悤�ɂقƂ�Ǖς�炸�C�����l�Ƃ͘������Ă��܂����ʂƂȂ����D��͂�ǕǂƂ̔M�`�B���l���ɓ����K�v������D
������C�̑S���xT0��293K���ɕۂ��C�Ǖlj��xTw��333K�C298K�C278K�̂R��ނɂ��ꂼ��ς��Ď����������ʗ��ʂƈ��͔�̊W�����C���C����ł��ꂼ�ꎦ�����̂��}�U�C�}�V�ł���D�������ʂɂ��ꂼ��Ή�����V�~�����[�V�����v�Z���ʂ��R�{�̋Ȑ��Ŏ����Ă���D���҂͂悢��v�������Ă���C�i�R�j���Œ�Ă����r���ߎ��ɂ��V�~�����[�V�������f���̗L�p�����m�F���ꂽ�D
�S�D������
��C���ǘH������ŊǕǂƂ̔M�`�B�̉e�����傫���ꍇ��ΏۂƂ������ʓ��������߂�ȒP�ȎZ�o�������������܂łɂ͂�����Ȃ��������C���̎����ɑ�������Ƃ��ē��Y�_���̓V�~�����[�V�����v�Z���f�����Ă������̂ŁC����ɕ��G�ȏ��������ł̃��f���̍\�z�ւ̑��|����ɂȂ�ƐM����D
���̒�N�ސE�҂ł��鏬�����������Ƃ����s�b�`�ł͂��邪�����̈�[��S���Ă���ꂽ�̂́C��w���E�̌����҂Ƃ̌p���I�Ȍ������͑Ԑ��ɂ����̂ł��邱�Ƃ���L�������D�܂��C�����ʼnY�H�Ƒ�w�@�C�m�w���ł������G���S��C�����m�C���x�˕��C��˗���̏��N���N���I�ɏ����֘A�����Ɍg���Ă����D���̐s�͑�ł��������Ƃ�t�L����D
�Q�l����
1) Gaitier, D., Chabane, S., Sesmat, S. and Hubert, D.: Long Pneumatic Tubes, Experimental Approach, ISO French Delegation Report 14 June, ISO/TC 131/SC 5/WG 3 N 613, p.1-11 (2010)
2) Notter, R. H. and Sleicher, C. A.: A solution to the turbulent Graetz problem-�V Fully developed and entry region heat transfer rates, Chemical Engineering Science, Vol. 22, p.2073-2093 (1972)
3) Nakano, K., Murayama, E. and Kawakami, Y.: On simplifications of simulation models for pneumatic turbulent flows through tubes, Proc. 9th JFPS Int. Sym. on Fluid Power, 3A1-4, p.702-707 (2014)
4) Kawashima, K., Ishii, T., Funaki, Y., and Kagawa, T.�FDetermination of flow rate characteristics of pneumatic solenoid valves using an isothermal chamber, Trans. ASME, J. Fluids Eng., Vol. 126, No.2, p.273-279 (2004)
���ҏЉ�

�Ȃ��̂�����
����a�v�@�N
1932�N1��13�����܂�D
1957�N�����H�Ƒ�w��w�@�C�m�ے��C��,���N�����H�w����������C�������C�������ւ�1992�N��N�ސE�C���H�喼�_�����C1992�N�ʼnY�H�Ƒ�w�����C2002�N��N�ސE�C���݂Ɏ���D���̐���̌����ɏ]���D���{�t���[�h�p���[�V�X�e���w��D
E-mail: k4-naka4(at)jcom.zaq.ne.jp
 �}�P�@�Ǔ���C���x�ω������ �j���FRe=10000�C��_�����FRe=40000 |
 �}�Q�@Simulink �u���b�N���} |
 �}�R�@�ߔM�E��p�p�����ǘH�\���ƊO�`�ʐ^ |
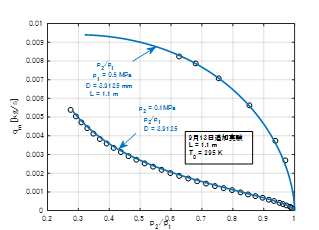 �}�S�@Fanno���ꃂ�f��Tw��T0�̏ꍇ |
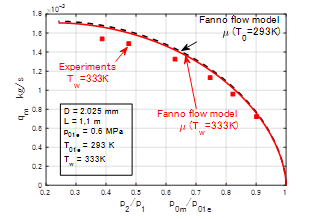 �}�T�@Fanno���ꃂ�f��T0��Tw=333K�̏ꍇ |
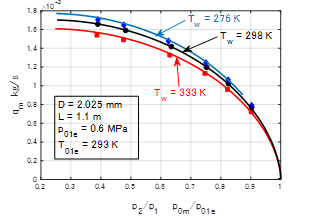 �}�U�@���a2mm�̓��� |
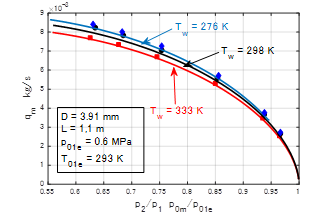 �}�V�@���a4mm�̓��� |