１．はじめに

この度は，栄誉ある日本フルードパワーシステム学会 SMC 高田賞を賜り，誠に光栄である．受賞論文「Flow patterns and Hysteresis characteristics of a Poppet Valve」の共著者である株式会社IHIの増田氏、九州工業大学の助教の清水先生、教授の淵脇先生、名誉教授の田中先生をはじめ，本研究にあたりお世話になった皆様に深く感謝申し上げる．本稿では，受賞対象論文の研究経緯と概要を紹介する．

２．研究背景

　ポペット弁は，油圧装置の制御弁としてスプール弁に次いでよく使用され，広く研究が行われている¹⁾．またポペット弁内のフローパターンは，スプール弁に比べ複雑な変化を示し，弁の動特性に影響を及ぼす要因の一つとなりうることが知られている．ポペット弁内の流れ場にはさまざまなフローパターンが存在して，それらが不安定振動と関連していることが理解されている^2)-7)が，それらの系統だった理解を得るには至っていない．増田ら⁸⁾は，ポペット弁の圧力－流量特性のヒステリシス現象を，弁の運動方程式と連成されたCFD解析により，再現可能であることを明らかにした．この研究結果は，CFDソフトウェアでポペット弁のヒステリシス特性を再現可能であることを示した興味深いものである．参考のため，増田らの研究⁸⁾において圧力－流量特性の実験結果とCFD計算結果を図1に示す．しかし残念ながら，彼らの研究ではヒステリシスとフローパターンとの詳細な関係までは述べられてはいない．本研究では，増田らの研究⁸⁾を引き継いでさらに発展させる目的で，彼らの研究で使用された試作ポペット弁内のフローパターンをCFD解析して系統的に整理するとともに，ヒステリシス特性とフローパターンの関係性について，さらにはそれらと流体力との関連を明らかにする．なお，CFDソフトウェアとしてSimerics MP+を利用した．

３．計算手法

Simerics-MP+ではCFD解析とともに弁体の運動方程式を連成して計算することもできる．計算格子は弁の並進運動に対応できるように，格子が伸縮可能なスライディングメッシュを使用した．これに有限体積法を適用することで，ポペット変位に伴う弁開度および流路形状の過渡的変化を反映したCFD解析が可能である．図2に供試ポペット弁の概略を示す．供試弁のスリーブポートは8か所であり，さらにその外側のケーシングにはドレンに向かう1か所の出口ポートが取り付けられている．また，図3に計算格子を，表1に計算条件を示す．本研究では，定常流計算と非定常流計算を行った．定常流計算では，弁を固定し，一定流量を与える条件を適用した．非定常計算では，弁を可動にして，流量をQ = 0.05 ~ 1.0 [ND]の範囲で線形に増大させ，その与えられた流量が定格流量に達すると，今度は逆に流量をQ = 1.0 ~ 0.05 [ND]の範囲で線形に減少させるという条件を適用した．非定常計算を行う際の初期条件は，まずは流量の初期値をQ = 0.05 [ND]と決めて，そのうえで弁を可動に設定して非定常計算を行い，弁の運動が落ち着いた状態での弁変位を初期値とした．この時の弁変位はx = 0.04 [ND]であった．

４．計算結果

4.1　フローパターン

図4に弁固定，流量一定の定常計算で得られた典型的な5種のフローパターン（一例，弁変位x = 0.07 [ND]の場合）を示す．各図は，ポペット軸を含む中央断面における速度コンター図を示している．なお，弁可動，流量変化の非定常計算の場合でもフローパターン2 ~ 5は確認できた．本研究では，計算格子の健全性を保つ関係上，初期弁変位を0.04 [ND]とした．

4.2　遷移現象

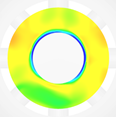
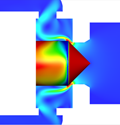
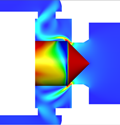
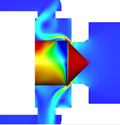
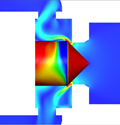
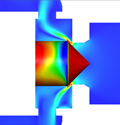
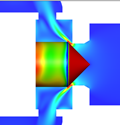
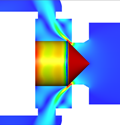
図1に示されたヒステリシス特性の軌跡の中で発生するフローパターン4から5への遷移の原因について，図5の参照平面①と②の上で検討する．参照平面①は，ポペットコーン終端部からポペットスプール開始の角部に発生しているはく離バブルを切断する円形断面として，参照平面②はポペット弁の軸を含む垂直断面として設定されている．このヒステリシス特性の遷移のメカニズムを特徴的に示唆している8枚の流れ場（同時刻の速度分布と圧力分布）のコンター図を，図6，7に示す．図6は参照平面①での圧力分布コンター図を示している．図7は参照平面②での内部流れの速度分布のコンター図であり，スロート部から弁室へ流入する噴流の様子がわかる．ただし，図7でのポペット弁体表面のカラーコンターは，その表面の圧力分布を示している．また，なお，以下の(a) ~ (h)のアルファベット記号は，図6, 7の記号に対応している．安定して存在する2つのフローパターン 4と 5（Attached flowとStraight flow）の間で，流量の増加に伴いフローパターンが遷移する原因は，(1) 流れ方向の変動とはく離，(2) 参照平面①に発生するはく離バブル（低圧部）の圧力分布の軸対称性が崩壊して流れの軸対称性が崩れること，(3) 参照平面②で見受けられるスロート直後の低圧部の出現，これらが同期して壁面付着流れからはく離流れが発生することによるものであることがわかった．これらのことから，ヒステリシス特性の経路とフローパターンの間には密接な関係があることがわかる．

4.3　ヒステリシスの経路に対応するフローパターンと流体力の関係

図1に示されるヒステリシスが発生している圧力－流量特性実験の作動領域での，流量変化に対する軸方向流体力とその際の弁変位に対する軸方向流体力を，図8(a)，(b)にそれぞれ示す．図8(a)に示される流量変化に対する軸方向流体力については，往路では，流量がQ = 0 [ND]あたりから増大し始めると負の流体力が徐々に増大して，流量Q = 0.69 [ND]あたりから流体力の不安定な変動が始まり，Q = 0.83 [ND]あたりで一気に正の流体力へと変化している．これはポペットスプールに付着した噴流が完全にはく離して，流れがカラーに衝突しなくなったためである．復路では，流量がQ = 1 [ND]あたりから減少し始めると，流体力は線形的に低下して，流量がQ = 0.42 [ND]を下回った付近で0 [ND]付近へと一気に低下する．また，その正負の流体力のオーダーは同程度である．つぎに，ヒステリシスとフローパターン，および軸方向流体力の関係性について考察する．参考のためFig. 15の経路上に，対応するフローパターンの番号を記入した．まず，流量Q = 0.25 [ND]以下の領域では，フローパターン 2， 3が現れる．その後，流量が増大して負の流体力が大きくなる（Q = 0.3 ~ 0.69 [ND]）領域ではフローパターン 4 （Attached flow）が現れる．さらに流量が増大すると，流体力の激しい振動が発生するが，この領域（Q = 0.69 ~ 0.83 [ND]）ではフローパターン 4とフローパターン 5の双方が入り乱れて現れており，わずかな擾乱を感じてフローパターンが遷移しようとしている領域である．この領域を通過するまで流量が増大すると，安定したフローパターン 5（Straight flow）が現れる．これより，フローパターン 4（Q = 0.3 ~ 0.69 [ND]）からフローパターン 5（Q > 0.83 [ND]）へ流れが遷移するとき（Q = 0.69 ~ 0.83 [ND]）は，流量は激しく振動することがわかる．図8(b)に示される弁変位に対する軸方向流体力についても同様の結果となる．往路で弁変位が徐々に大きくなるのは，フローパターン4の壁面付着した流れがカラーに衝突して流量の増加とともなって負の流体力を増大させるからである．また，弁変位x = 0.8 ~ 0.95 [ND]あたりでの流体力の大きな変動域では，弁が前後に小刻みに変動していることがわかる．これは，4.2節で紹介した，(3) 参照平面②で見受けられるスロート直後の低圧部の出現とも関連していると考えてよい．復路では弁変位と流体力は線形的に低下している．また，同じ弁変位でも往路と復路に対応するフローパターンが存在していることもわかる．以上，ヒステリシス特性はフローパターンが 4（Attached flow）と 5（Straight flow）との間で遷移を起こすことによるものであることがわかった．その遷移には，速度場の変化，圧力分布の軸対称性の崩壊，スロート直後の低圧部の出現，これらと同期して弁変位が変動することが深く関係していることがわかった．その結果，フローパターンが変化して，流体力の極性が負（－）から正（＋）へと違った極性になることもわかった．

５．おわりに

本研究では，CFDソフトウェアを利用して，増田ら⁸⁾の研究で使用された試作ポペット弁内のフローパターンを系統的に整理し，ヒステリシス特性とフローパターンの関係性について明らかにした．ポペット弁のヒステリシス特性の経路はフローパターン，およびそれに同期する圧力分布や速度分布，ならびに流体力の変動に基づく弁変位の変化と密接な関係があることがわかった．

参考文献

1) 大島，市川常雄：ポペット弁に作用する非定常流体力の測定, 日本機械学会論文集（B編）,49-447，p2473-2477 (1978).

2) Schrenk E.:Disc Valves, Flow Patterns, Resistance, and Loading, British Hydromechanics Research Association, 547, p.1-17 (1957).

3) McCloy, D. and McGuigan, R.H. : Some static and dynamic characteristics of poppet valves, Proc. Instn. Mech. Engrs, 179, p199-213(1964).

4) Johnston, D. N., Edge, K. A.: Experimental investigation of flow and force characteristics of hydraulic poppet and disc valves, Proc. Instn. Mech. Engrs, Part A, 205, p161-171 (1991).

5) Vaughan, N. D., et. al.: Numerical simulation of fluid flow in poppet valves, Proc. Instn. Mech. Engrs, Part A, 206, 119-127(1992).

6) Hayashi, S.: Instability of Poppet Valve Circuit, JSME international journal. Ser. C, Dynamics, control, robotics, design and manufacturing, 38-3, p357-366 (1995).

7) Altare, G., Rundo, M., Olivetti, M.: 3D dynamic simulation of a flow force compensated pressure relief valve, Proc. Instn. Mech. Engrs Congress and Exposition IMECE2016 November 11-17, IMECE2016-65624 (2016).

8) 増田，清水，渕脇，田中：ポペット弁型圧力制御弁の内部流れ，解析とヒステリシスの再現，日本フルードパワーシステム学会論文集，52-1，p8-15(2021)．

著者紹介

ひろせ　　なおき

廣瀬　直紀　君

2021年九州工業大学大学院博士前期課程修了．日本フルードパワーシステム学会の会員．

E-mail: p237060n(at)gmail.jp

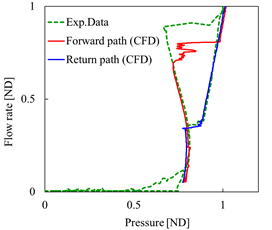図1 圧力－流量特性のヒステリシス経路（実験結果とCFD計算結果の比較）（出典：文献(8)）

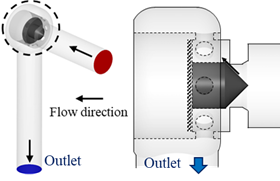図2 試作ポペット弁概略図

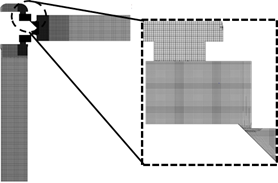図3 計算格子

表1 計算条件

Software used	Simerics-MP+
Analysis type	Steady state	Transient
Turbulence model	Standard k-ε
Fluid density	770
Fluid viscosity	0.00149
Entrance boundary condition [ND]	Flow rate = const.	0.05~1 (Flow rate/Rated flow rate )
Exit B.C. [ND]	0.2 (Static Pressure)
Grid number	4,000,000 [-]
Incremental time		0.000054 [s]

(a) Flow pattern 1	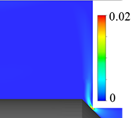(b) Flow pattern 2	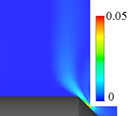(c) Flow pattern 3 (Unstable flow)	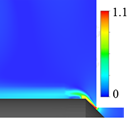(d) Flow pattern 4 (Attached flow)	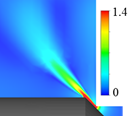(e) Flow pattern 5 (Straight flow)

図4 典型的な5種のフローパターン

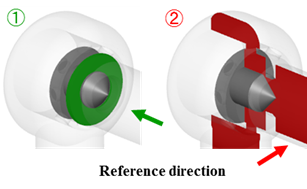図5 参照平面

(a) t = 0.391 [s]	(b) t=0.427 [s]	(c) t = 0.433 [s]	(d) t = 0.435 [s]
(e) t = 0.448 [s]	(f) t = 0.461 [s]	(g) t = 0.463 [s]	(h) t = 0.471 [s]
図6 参照面①における圧力分布の時系列データ

(a) t = 0.391 [s]	(b) t=0.427 [s]	(c) t = 0.433 [s]	(d) t = 0.435 [s]	ポペット弁体
(e) t = 0.448 [s]	(f) t = 0.461 [s]	(g) t = 0.463 [s]	(h) t = 0.471 [s]	弁室
図7 参照面②における圧力分布と速度分布の時系列データ

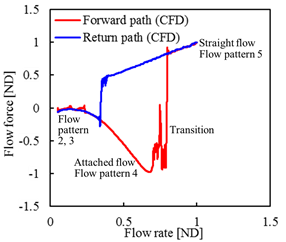(a) 流量変化に対する軸方向流体力	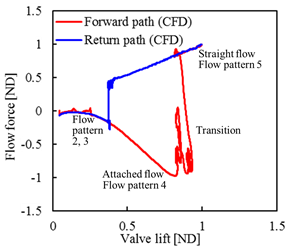(b) 弁変位に対する軸方向流体力
図8 軸方向流体力の時系列データ