１．はじめに

この度は名誉あるSMC高田賞を賜り，まことに光栄である．受賞論文は「Ultra Precise Positioning Control for Rotary Pneumatic Actuator (Simultaneous Improvement on Transient and Steady State Performance)」であり，本論文の共著者である徳島大学の高岩昌弘教授に心より感謝申し上げる．本稿では受賞論文の研究について，その背景や概要を紹介させていただく．

２．研究背景

　本稿は，一般的なラバーシールを備えた市販の回転式空気圧アクチュエータに対し，従来の制御手法では容易でなかった超高精度の位置決め制御を実現するための新たな補償器とフィードフォワード制御を組み合わせた手法について解説するものである．空気圧アクチュエータは，シンプルな構造のためメンテナンス性がよく，低コスト，安全・クリーンなどのメリットを有する反面，空気の高圧縮性や非線形摩擦の影響によるスティック・スリップ現象のため，高精度な位置決め用途には限定的な状況である．これに対し，従来の研究ではエアーべアリングによるハードウエア的な対応が一般的であるが，多くの場合，高価な装置投資が必要であった．本研究では，摩擦の影響を顕著に受ける汎用型ロータリアクチュエータに対して，提案する補償器による定常状態における位置決め精度の改善と，フィードフォワード制御による過渡応答の最適化に対するアプローチについて説明する．

３．制御システムの概要

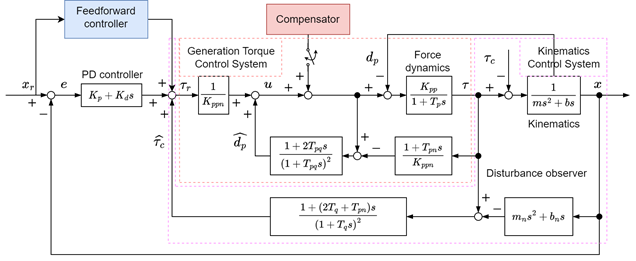
図1に位置制御系を示す．外乱オブザーバとPD制御系を用いたフィードバック部による外乱抑圧特性と，フィードフォワードの導入による目標値追従特性を独立して設計可能な2自由度制御系の構成になっている．フィードバック制御部では，発生トルクから回転角度までの伝達部に外乱オブザーバを導入し，外乱として作用する摩擦トルクやプラントパラメータ変動の影響をトルクの次元で推定する．この推定されたトルクを相殺するトルクを生成するために，内部に新たにトルク制御系が構成されている．内部のトルク制御系にも外乱オブザーバが構成されており，制御信号から発生トルクまでの伝達部の非線形性の補償と，等価的に外乱として作用する回転角速度の影響の除去を目的としている．制御信号には提案する高精度化補償器の出力信号が重畳されており，これによりスティック・スリップが抑制され，定常域における高精度な繰り返し位置決め精度が担保される．

一方，PD制御器の出力から角速度までの伝達部において２型の制御系となるように外乱オブザーバのフィルタ構造を構成することで，その伝達部のダイナミクスを粘性項だけでなく慣性項までノミナルモデルに固定できる．そのため，フィードフォワード要素にその逆モデルを構成することで，ダイナミクスキャンセルを行い，目標軌道への追従性能を高める．

実験結果からは，補償器が定常状態でのスティック・スリップ現象を大幅に低減し，フィードフォワード制御によるダイナミクス補償が負荷変動時のロバスト性を含め，過渡応答における目標軌道追従特性を向上させることが明らかとなった．

４．実験結果と評価

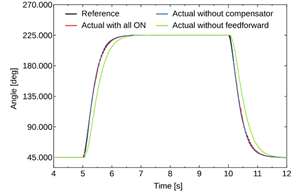
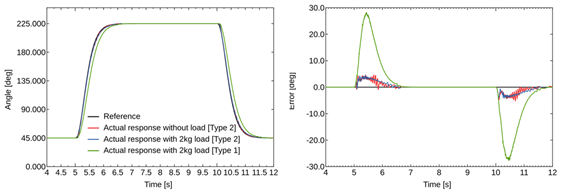
図2は，変位角度180°のステップ応答結果を示している．本実験では，補償器とフィードフォワード制御が有効な場合（赤色の線）と，いずれかの制御要素が欠如した場合（青色または緑色の線）との応答が比較され，補償器が定常状態でのスティック・スリップ現象を低減し，過渡領域における応答の改善が明確に確認された．補償器が作用するにつれて，アクチュエータが目標角度に対して迅速かつ正確に収束する様子が示されている．

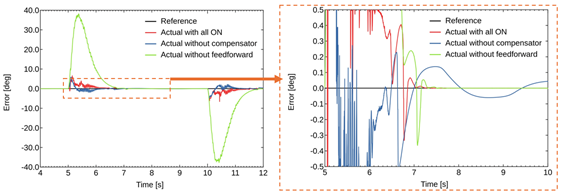
図3では，図2の実験における誤差グラフを示す．補償器とフィードフォワード制御が組み合わされた場合に定常状態での角度誤差が大幅に減少し，図からは読み取れないが誤差は±1/10,000°の位置決め精度が実現された．

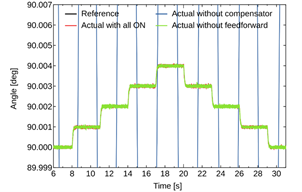
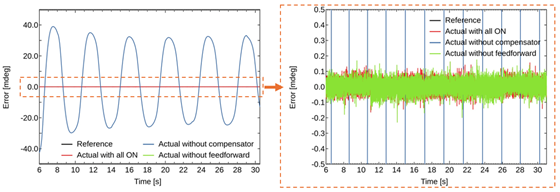
図4は，1/1000°ステップ応答実験の結果を示す．図5では，補償器とフィードフォワード制御が有効な場合（赤色の線）と，各制御要素が欠如した場合（青色や緑色の線）との比較が行われ，特にこのように非常に小さなステップ応答においてはダイナミクスの問題は無視できるためフィードフォワード制御の効果は限定的である一方，補償器の効果により非常に細かなステップ追従を可能としている．図5より，過渡状態と定常状態の全時間帯域において誤差は約±1/10,000°に収まっている．

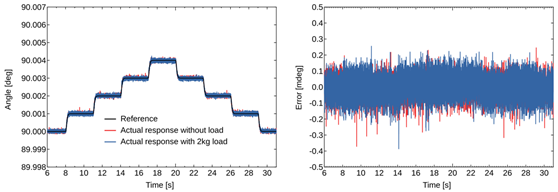
さらに，図6と図7は，2kgの外部負荷を加えた場合のステップ応答結果である．図6では，負荷の有無にかかわらず，補償器とフィードフォワード制御が組み合わされた場合において，目標角度に対する追従性能がほぼ同一であることが確認され，システムのロバスト性が実証された．緑線で示される従来の１型の制御系では，過渡応答中に偏差が見られるのに対し，青線のタイプ2の制御系は外乱負荷に対してもロバストな挙動を示している．加えて，図7では，1/1000°ステップ応答実験における誤差が極めて小さい範囲内に収まっていることから，外部負荷下においても高精度が維持されることが明示されている．

以上の実験結果は，システム全体の各ブロックが有機的に連携し，従来の制御手法では達成が困難であった過渡応答および定常状態での高精度位置決めが実現されることを示しており，今後の応用や製造現場における実用の可能性を示すものと言える．

５．おわりに

本研究は，一般的な市販部品を活用した回転式空気圧アクチュエータに対し，高精度化補償器とフィードフォワード制御器を組み合わせる新たな位置決め制御手法を提案するものである．実験により，定常状態および過渡応答において高い位置決め精度とロバスト性を実現したことが確認され，今後の産業応用への展開が期待される．

参考文献

1） D. Saravanakumar, B. Mohan, and T. Muthuramalingam. A review on recent research trends in servo pneumatic positioning systems. Precision Engineering, 49:481–492, 2017.

2） Ke Li, Yeming Zhang, Shaoliang Wei, and Hongwei Yue. Evolutionary algorithm-based friction feedforward compensation for a pneumatic rotary actuator servo system. Applied Sciences, 8(9), 2018.

3） Toshinori Fujita, Kazutoshi Sakai, Yusuke Takagi, Kenji Kawashima, and Toshiharu Kagawa. Ultra precise positioning of a stage driven by pneumatic bellows. International Journal of Automation Technology, 5:508–515, 2011.

4） M. Hayashi, H. Sawano, H. Yoshioka, and Hidenori Shinno. Torque error compensation in pneumatic rotary actuator system using an electromagnetic force. Proceedings of the 5th International Conference on Leading Edge Manufacturing in 21st Century, LEM 2009, 2009.

5） Behrad Rouzbeh, Gary M. Bone, Graham Ashby, and Eugene Li. Design, implementation and control of an improved hybrid pneumatic-electric actuator for robot arms. IEEE Access, 7:14699–14713, 2019.

6） Takaiwa Masahiro and Noritsugu Toshiro. Positioning control of pneumatic parallel manipulator. International Journal of Automation Technology, 2(1):49–55, 2008.