１．はじめに

この度は名誉あるSMC高田賞を賜り，誠に光栄である．受賞論文は「Concurrent Learningに基づく水圧人工筋の線形近似モデルと適応変位制御」であり，本論文の共著者である芝浦工業大学の伊藤和寿教授をはじめ，本研究にご協力いただいた関係者の皆様に心より感謝申し上げる．本稿では受賞論文の研究について，その背景と概要を紹介させていただく．

２．研究背景

　水圧駆動人工筋は，軽量，安価で高パワー密度，環境負荷が小さいなどの人工筋と水圧システムのメリットを併せ持つアクチュエータであるため，環境負荷の低減化が要求されるような様々な分野で応用が期待されている¹⁾．しかしながら，非対称なヒステリシス特性を持つ人工筋はモデル化や制御系設計が容易ではないため，その非線形性を補償する制御系の設計は応用範囲拡大のために重要な課題である．

近年の制御系設計はモデルベース制御，データ駆動型制御の2つに大別することができる²⁾．人工筋システムの制御においても例外ではなく，非対称Bouc-Wenモデルに基づくモデル化と非線形補償およびモデル予測制御系で構築されるモデルベース制御³⁾，数学モデルを陽に用いずに，事前実験データから直接制御器を調整する手法⁴⁾，各時間ステップにのみ対応する仮想的なモデル表現とそれに基づくモデルフリー適応制御⁵⁾（以下，MFAC），Ultra localモデルに基づく制御⁶⁾などに代表されるデータ駆動型制御，など多くの制御系が提案されている．しかしながら，前者では数学モデルの導出，同定，評価に大きな工数がかかり，後者では事前実験データの質や目標軌道に対して大きな制限を持つなど，それぞれ実応用上の問題が存在する．

本研究では，この問題に対し，数学モデルを簡易的なモデルとして近似し，モデル化できない動特性が常に存在することを前提とした適応制御系の設計を検討した．特に，持続的励起⁷⁾（以下，PE）条件と呼ばれる同定入力の一般的な条件を仮定せずにパラメータの収束性や安定性を議論できるConcurrent Learning⁸⁾（以下，CL）に着目し，Directional Forgetting⁹⁾（以下，DF）と組み合わせることで，モデル化できない動特性に対してロバストな新しい離散時間間接適応制御系を提案した．本成果では，入出力関係のみから表現される線形ARXモデルを導入して，人工筋の非対称ヒステリシスをモデル化できない動特性として取り扱うことで，ある種のデータ駆動型アプローチの側面を持ち，上述のデメリットを抑制したモデルベースとデータ駆動の融合制御手法と位置付けられる．つまり，本提案手法は制御中の入出力情報と線形モデルの構造のみを必要としており，事前のシステム同定が不要であるほか，任意の目標軌道に対する追従制御系の設計が期待できる．

３．Concurrent Learning適応制御系の設計

時刻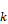，人工筋変位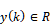，制御入力（比例弁への印加電圧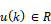）とすると，人工筋システムはつぎのように表現できる．

ただし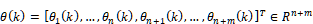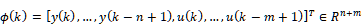，，はそれぞれパラメータベクトル，リグレッサベクトルを表す．また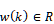，はモデル化できない動特性および外乱を表し，有界であるがその大きさは未知であると仮定する．本研究では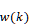，は非対称ヒステリシス項に該当する．よって，線形ARXモデルにより人工筋システムを近似すると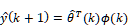，と表せる．ただし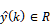，は予測出力であり人工筋の変位自体ではないことに注意する．また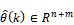，は推定パラメータベクトルである．したがって，推定パラメータ誤差を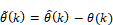として定義すると，同定誤差は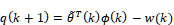として表せる．

　線形ARXモデルに対し，提案のDF-CL法におけるパラメータ更新則は正規化勾配（以下，NG）法の更新則に蓄積データの誤差を表現した第三項目を追加することで，つぎのように表せる．

ただし，でありは情報行列，は補助ベクトルを表し，以下のAlgorithm 1によってそれぞれ更新される．また，は学習ゲインを表し，

を満たすように時変で設計する．

Algorithm 1 Update law of using DF
Input:
Output:
	for all do
		If then
			,
		Else
			,

		End if
	End for

つぎに，適応制御則はDF-CL法によって推定されたパラメータベクトルを利用して，つぎのように表せる．

ただし，は設計者が任意に設計する参照モデル出力であり，は出力と参照デル出力との誤差である．は誤差の収束速度を表す設計パラメータであり，の範囲で設計する．さらに，式(3)のゼロ割を防ぐために，を満たすような不感帯も導入する．

　提案手法は，情報行列の列フルランク性が満たされると仮定すると，モデル化できない動特性が存在しなかった場合にはパラメータ誤差と追従誤差は指数安定性を保証され，モデル化できない動特性が存在し，その値が有界である場合には，DFの導入とその拡張によって効果的に外乱の影響を抑制することで，パラメータ誤差と追従誤差の一様終局有界性が保証される¹⁰⁾．

４．数値シミュレーション結果および考察

まず，モデル化できない動特性が存在しない条件下で評価を実施するため，人工筋の線形ARXモデル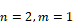（）に対して，同様の構造を用いてNGおよびDF-CLに基づき間接適応制御系を設計し，それらの制御性能を比較する．次に，モデル化できない動特性の影響を考慮するために，シミュレーションモデルを人工筋の特性を高精度に表現した非対称Bouc-Wenモデル（負荷44 Nにより同定）とし，制御系設計に用いる数学モデル構造は線形ARXモデル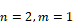（）のまま設定した．加えて，データ駆動型制御の中でも人工筋の変位制御系として十分に有効性が確認されており，NG法を適応推定機構としてもつMFACとも比較することで，提案手法の有効性をより詳細に評価する．なお，図. 1には水道水圧駆動人工筋で用いる水圧回路および実験装置の外観をそれぞれ示す．

本シミュレーションでは，サンプリング時間を0.01 s，を時間シフトオペレータとし，参照モデルは，不感帯幅は，設計パラメータはにそれぞれ設定した．さらに，パラメータの初期値はすべて0，重みは最適な更新となるように制約範囲の上界の半分で時変，忘却要素でそれぞれ設定した．ただし，忘却係数の設定については試行錯誤が必要であり，の値が1に近いほど忘却性能が高いことに注意する．本研究においてはまた，MFACは入出力の変化量の次数を同様に設定し，それに対応する疑似勾配ベクトル（勾配法におけるパラメータベクトルに対応する）の初期値は，入力の変化量に対する重みを5，その他の値をすべて1に，それぞれ設定した．

モデル化できない動特性が存在しない場合の制御結果および推定パラメータの比較を図. 2に示す．この制御結果より，NGおよびDF-CLの両者の手法とも定常応答において十分な制御性能が得られていることが確認できる．一方で，過渡応答においては提案手法のみが制御性能の改善を達成している．間接適応制御系では，推定パラメータが真値であることを前提とするCertainty Equivalence原理に基づき設計されているため，パラメータの真値収束が重要である．しかしながら，一般にPE条件を満たさない場合には真値収束の達成は保証されず，その条件は同定入力や目標軌道に依存するため，この条件を満足することは実応用上容易ではない．提案手法は非PE条件下にも関わらず，図. 2 (b)に示すように各推定パラメータが真値へ収束していることがわかり，このことから制御性能の改善は妥当であると考えられる．一方，従来手法はPE性を満たさないためにパラメータが真値へ収束せず，目標軌道が変化するたびにパラメータ更新に影響が発生するため，過渡性能が劣化していると考えられる．

　次に，非対称ヒステリシス項をモデル化できない動特性として扱い，線形ARXモデルに基づいて適応制御器を設計した結果およびそのときのパラメータ誤差のノルムの比較を図. 3，平均絶対誤差による評価結果をTable 1にそれぞれ示す．従来手法は目標軌道が変化する過渡応答において大きなオーバーシュートや振動的な応答が見られる．一方，提案手法はモデル化できない動特性が存在するにもかかわらずほとんど制御性能が劣化せず，過渡応答を大幅に改善できることが明らかになった．この結果は，図. 3 (b)において，提案手法のパラメータ誤差のノルムが十分小さい値で有界であることからも妥当であると考えられる．また，MFACはNG法ほどオーバーシュートが発生しないものの，特に目標軌道が正弦波の区間において十分に追従性能を発揮することができていない．これは，MFACの追従誤差の漸近安定性が，目標軌道が一定の場合に限定されるためである．このように，データ駆動型制御の一つであるMFACは対応可能な目標軌道に制限があり，設計者が任意に設計することができない一方，提案手法は様々な目標軌道に対して追従することができる上に，主に設計するべきパラメータはモデル構造の次数のみであるため，設計工数の削減も達成された．

５．おわりに

　本稿では，Directional ForgettingとConcurrent Learningを組み合わせた，水圧人工筋の変位制御系に対する新しい離散時間間接適応制御系について紹介し，受賞論文の概要について簡単に述べた．提案した制御系は，非対称ヒステリシスをモデル化できない動特性として扱い，線形ARXモデル構造のみから制御系を設計できるため事前のシステム同定が不要であり，モデルベースとデータ駆動の特長を併せ持つ融合手法として位置づけられる．一方で，パラメータの真値収束速度はかなり遅く，サンプリング時間を粗くした場合にはその結果が顕著に表れ，過渡性能の劣化につながる恐れがある．この問題に対して，著者らはその後の研究において，提案手法を逐次最小二乗問題へ拡張した二層忘却型RLS法¹¹⁾と呼称する新しい適応同定手法を提案しており，その有効性も検証している．今後はこれらの水圧人工筋への適用および実験的な評価についても検討していきたい．

参考文献

1）小林亘，伊藤和寿 : 水道水圧駆動マッキベン型人工筋の変位制御（第1報，人工筋のモデル化およびBouc-Wenモデルの適用）, 日本フルードパワーシステム学会論文集, Vol. 45, No. 6, p. 85-93, (2014)

2） Hou, Z., Zhuo W.: From Model-Based Control to Data-Driven Control: Survey, Classification and Perspective, Information Sciences Vol. 235, p. 3-35, (2013).

3） Tsuruhara, S., Inada, R., Ito, K.: Model predictive displacement control tuning for tap-water-driven artificial muscle by inverse optimization with adaptive model matching and its contribution analyses, International Journal of Automation Technology Vol. 16, No. 4, p. 436-447, (2022)

4） Takada, S., Kaneko O., Nakamura, T., Yamamoto S.: Data-driven tuning of nonlinear internal model controllers for pneumatic artificial muscles, 2014 4th Australian Control Conference (AUCC), p. 13-18, (2014)

5） Tsuruhara, S., Ito, K.: Data-driven model-free adaptive displacement control for tap-water-driven artificial muscle and parameter design using virtual reference feedback tuning, Journal of Robotics and Mechatronics Vol. 34, No. 3, p. 664-676, (2022)

6） Kosugi, A., Tsuruhara, S., Sekine, M., Ito, K., Zobel, P. B., Durante, F.: Ultra-Local Model Based Data-Driven Control for McKibben-type Artificial Muscles with Control Parameter Optimization Using VRFT, Proc. of 12th JFPS International Symposium on Fluid Power in Hiroshima 2024, 1B2-03, (2024)

7） Gang, T., Adaptive Control Design and Analysis, John Wiley & Sons, (2003)

8） Chowdhary, G., and Eric, J.: Concurrent Learning for Convergence in Adaptive Control without Persistency of Excitation, In 49th IEEE Conference on Decision and Control (CDC), p. 3674–79, (2010)

9） Cao, L., Howard, S.: A Directional Forgetting Algorithm Based on the Decomposition of the Information Matrix, Automatica, Vol. 36, No. 11, p. 1725-1731, (2000)

10） Tsuruhara, S., Ito, K.: Discrete-time Indirect Adaptive Control for Systems with Disturbances via Directional Forgetting: Concurrent Learning Approach, arXiv preprint arXiv:2409.09316, (2024)

11） Tsuruhara, S., Ito, K.: Discrete-time Two-Layered Forgetting RLS Identification under Finite Excitation, arXiv preprint arXiv:2504.19518, (2025)

著者紹介

つるはら　さとし

鶴原　理司　君

2023年芝浦工業大学大学院理工学研究科機械工学専攻修了．同年同大学院博士後期課程機能制御システム専攻入学，日本学術振興会特別研究員（DC1），現在に至る．水圧・油圧システム制御，適応制御理論，データ駆動型制御理論とその応用研究に従事．日本フルードパワーシステム学会，計測自動制御学会の会員．修士(工学)．

E-mail: nb23110(at)shibaura-it.ac.jp

URL: https://tsuruhara.net

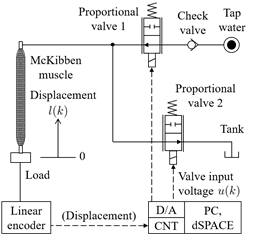(a) 水圧回路	(b) 実験装置外観
図1　水道水圧駆動人工筋システム

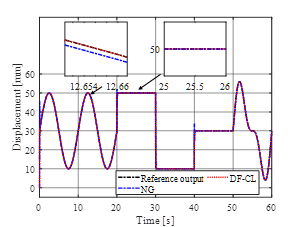(a) 制御性能の比較	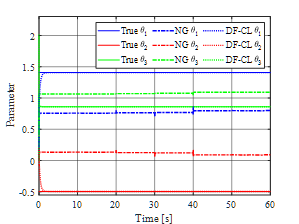(b) 推定パラメータの比較
図2　線形ARXモデルに対する性能比較（モデル化できない動特性なし）

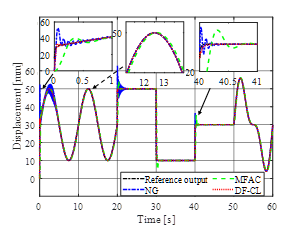(a) 制御性能の比較	(b) 推定パラメータの比較
図3　非対称Bouc-Wenモデルに対する性能比較（モデル化できない動特性あり）

表1 平均絶対誤差による制御性能の比較（モデル化できない動特性あり/なし）